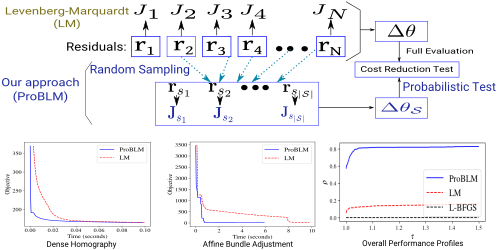
Abstract:
Top-k maximum inner product search (MIPS) is a central task in many machine learning applications. This work extends top-k MIPS with a budgeted setting, that asks for the best approximate top-k MIPS given a limited budget of computational operations. We investigate recent advanced sampling algorithms, including wedge and diamond sampling, to solve budgeted top-k MIPS. First, we show that diamond sampling is essentially a combination of wedge sampling and basic sampling for top-k MIPS. Our theoretical analysis and empirical evaluation show that wedge is competitive (often superior) to diamond on approximating top-k MIPS regarding both efficiency and accuracy. Second, we propose dWedge, a very simple deterministic variant of wedge sampling for budgeted top-k MIPS. Empirically, dWedge provides significantly higher accuracy than other budgeted top-k MIPS solvers while maintaining a similar speedup.