Abstract:
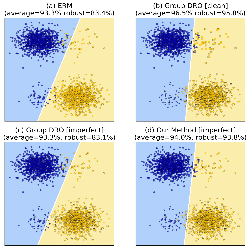
Complex classification performance metrics such as the F-measure and Jaccard index are often used, in order to handle class-imbalanced cases such as information retrieval and image segmentation. These performance metrics are not decomposable, that is, they cannot be expressed in a per-example manner, which hinders a straightforward application of M-estimation widely used in supervised learning. In this paper, we consider linear-fractional metrics, which are a family of classification performance metrics that encompasses many standard ones such as the F-measure and Jaccard index, and propose methods to directly maximize performances under those metrics. A clue to tackle their direct optimization is a calibrated surrogate utility, which is a tractable lower bound of the true utility function representing a given metric. We characterize sufficient conditions which make the surrogate maximization coincide with the maximization of the true utility. Simulation results on benchmark datasets validate the effectiveness of our calibrated surrogate maximization especially if the sample sizes are extremely small.