Abstract:
We introduce a randomly extrapolated primal-dual coordinate descent method that automatically adapts to the sparsity of the data matrix as well as the favorable structures of the objective function in optimization.
Our method can update only a subset of primal and dual variables with sparse data, and it can provably use large step sizes with dense data, retaining the benefits of the specific methods designed for each case.
In addition to key adaptivity to the sparsity, our method attains fast convergence guarantees in favorable cases \textit{without any modifications}. In particular, we prove linear convergence under metric subregularity, which applies to strongly convex-strongly concave problems, linear programs and piecewise linear quadratic functions.
We also show almost sure convergence of the sequence and optimal sublinear convergence rates for the primal-dual gap and objective values in the worst case.
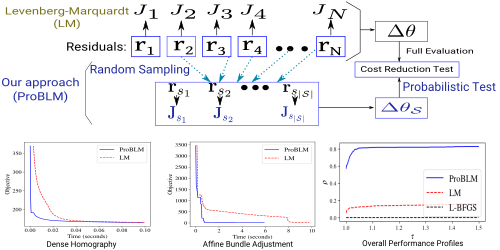
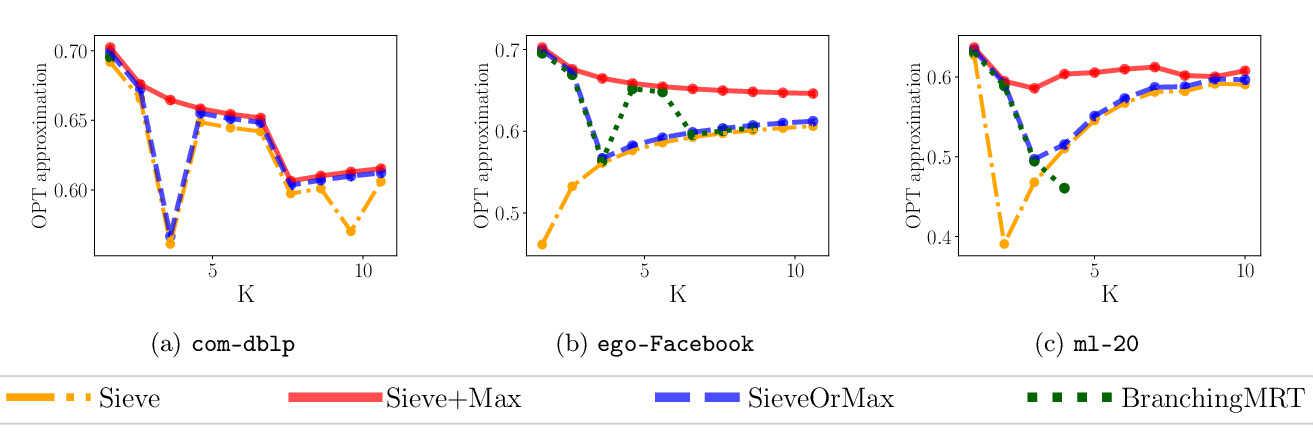
Numerical evidence demonstrates the state-of-the-art empirical performance of our method in sparse and dense settings, matching and improving the existing methods over different applications with real data.