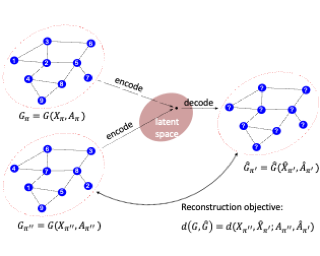
Abstract:
Most of the successful deep neural network architectures are
structured, often consisting of elements like convolutional neural
networks and gated recurrent neural networks. Recently, graph neural
networks (GNNs) have been successfully applied to graph-structured data such
as point cloud and molecular data. These networks often only consider
pairwise dependencies, as they operate on a graph structure. We
generalize the GNN into a factor graph neural network
(FGNN) providing a simple way to incorporate dependencies among
multiple variables. We show that FGNN is able to represent
Max-Product belief propagation, an approximate inference method on
probabilistic graphical models, providing a theoretical understanding on the capabilities of FGNN and related GNNs. Experiments on synthetic and real datasets demonstrate the potential of the proposed architecture.