Abstract:
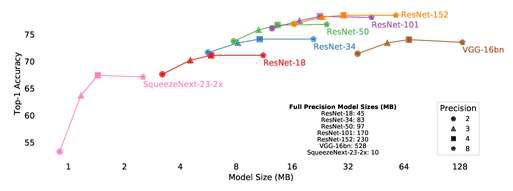
We propose layer saturation - a simple, online-computable method for analyzing the information processing in neural networks. First, we show that a layer’s output can be restricted to an eigenspace of its covariance matrix without performance loss. We propose a computationally lightweight method that approximates the covariance matrix during training. From the dimension of its relevant eigenspace we derive layer saturation- the ratio between the eigenspace dimension and layer width. We show evidence that saturation indicates which layers contribute to network performance. We demonstrate how to alter layer saturation in a neural network by changing network depth, filter sizes and input resolution. Finally we show that pathological patterns of saturation are indicative of parameter inefficiencies caused by a mismatch between input resolution and neural architecture.