Abstract:
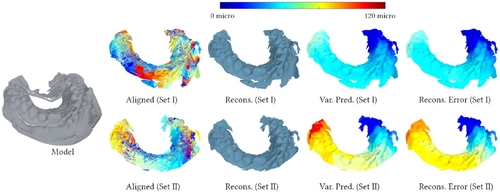
Recent frameworks for image denoising have demonstrated that it can be more productive to recover an image from a smoothed version of some geometric feature of the image rather than denoise an image directly. Improvements can be found both with respect to image quality metrics as well as the preservation of fine details. The challenge in working with this data is that mathematically sound mechanisms developed for handling natural image data do not necessarily apply, and this data itself can be quite ill behaved. In this work we learn both `geometric' or nonlinear higher order features and corresponding regularizers. These approaches show improvement over state-of-the-art deep learning (DL) based image denoising methods. Furthermore, the proposed DL architecture is motivated by and has the potential to feed back into mathematically sound models to solve a variety of image processing problems.