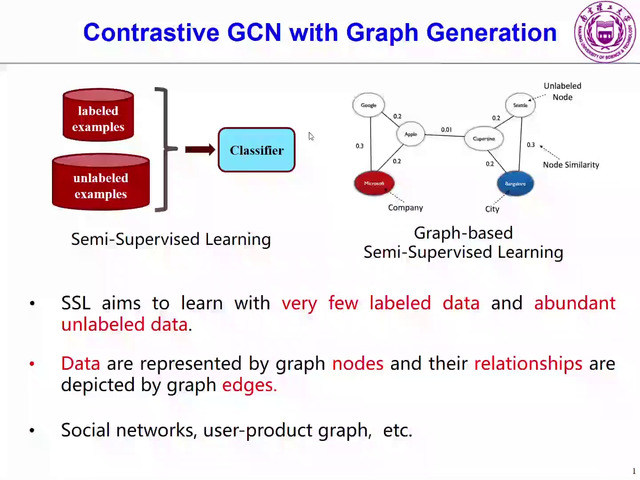
Abstract:
A recent Wasserstein Weisfeiler-Lehman (WWL) Graph Kernel has a distinctive feature: Representing the distribution of Weisfeiler-Lehman (WL)-embedded node vectors of a graph in a histogram that enables a dissimilarity measurement of two graphs using Wasserstein distance. It has been shown to produce better classification accuracy than other graph kernels which do not employ such distribution and Wasserstein distance. This paper introduces an alternative called Isolation Graph Kernel (IGK) that measures the similarity between two attributed graphs. IGK is unique in two aspects among existing graph kernels. First, it is the first graph kernel which employs a distributional kernel in the framework of kernel mean embedding. This avoids the need to use the computationally expensive Wasserstein distance. Second, it is the first graph kernel that incorporates the distribution of attributed nodes (ignoring the edges) in a dataset of graphs. We reveal that this distributional information, extracted in the form of a feature map of Isolation Kernel, is crucial in building an efficient and effective graph kernel. We show that IGK is better than WWL in terms of classification accuracy, and it runs orders of magnitude faster in large datasets when used in the context of SVM classification.