Abstract:
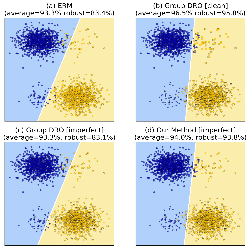
Data containing human or social features may over- or under-represent groups with respect to salient social attributes such as gender or race, which can lead to biases in downstream applications. Prior approaches towards preprocessing data to mitigate such biases either reweigh the points in the dataset or set up a constrained optimization problem on the domain to minimize a metric of bias. However, the former do not learn a distribution over the entire domain and the latter do not scale well with the domain size. This paper presents an optimization framework that can be used as a data preprocessing method towards mitigating bias: It can learn distributions over large domains and controllably adjust the representation rates of protected groups and/or achieve target fairness metrics such as statistical parity, yet remains close to the empirical distribution induced by the given dataset. Our approach appeals to the principle of maximum entropy, which states that amongst all distributions satisfying a given set of constraints, we should choose the one closest in KL-divergence to a given prior. While maximum entropy distributions can succinctly encode distributions over large domains, they can be difficult to compute. Our main technical contribution is an instantiation of the maximum entropy framework for our set of constraints and priors, which encode our bias mitigation goals, that runs in time polynomial in the dimension of the data. Empirically, we observe that samples from the learned distribution have desired representation rates and statistical rates, and when used for training a classifier incurs only a slight loss in accuracy while maintaining fairness properties.