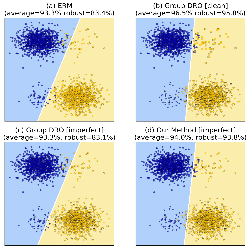
Abstract:
It is well known that vision classification models suffer from poor calibration in the face of data distribution shifts. In this paper, we take a geometric approach to this problem. We propose Geometric Sensitivity Decomposition (GSD) which decomposes the norm of a sample feature embedding and the angular similarity to a target classifier into an instance-dependent and an instance-independent com-ponent. The instance-dependent component captures the sensitive information about changes in the input while the instance-independent component represents the insensitive information serving solely to minimize the loss on the training dataset. Inspired by the decomposition, we analytically derive a simple extension to current softmax-linear models, which learns to disentangle the two components during training. On several common vision models, the disentangled model out-performs other calibration methods on standard calibration metrics in the face of out-of-distribution (OOD) data and corruption with significantly less complexity. Specifically, we surpass the current state of the art by 30.8% relative improvement on corrupted CIFAR100 in Expected Calibration Error.