Abstract:
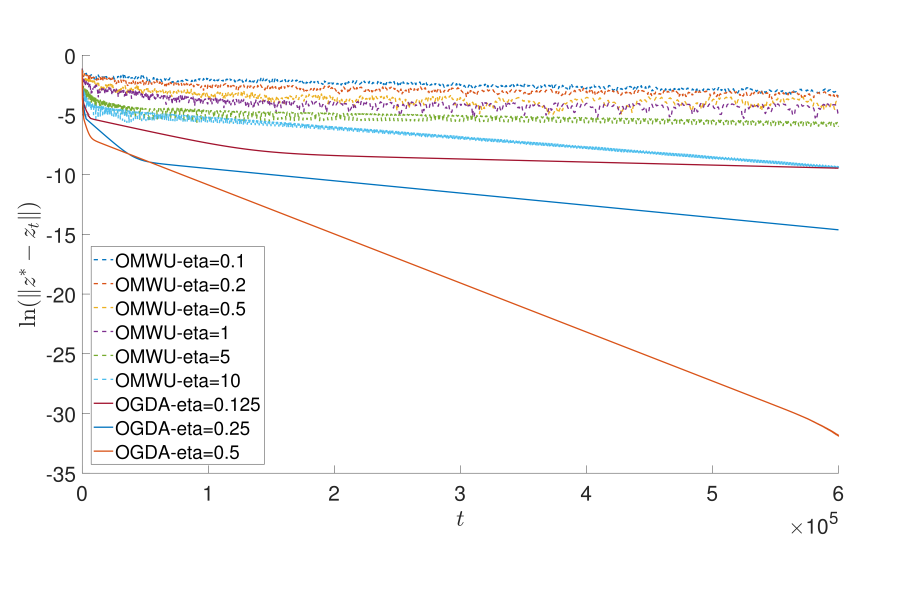
We study the question of obtaining last-iterate convergence rates for no-regret learning algorithms in multi-player games. We show that the optimistic gradient (OG) algorithm with a constant step-size, which is no-regret, achieves a last-iterate rate of O(1/√T) with respect to the gap function in smooth monotone games. This result addresses a question of Mertikopoulos & Zhou (2018), who asked whether extra-gradient approaches (such as OG) can be applied to achieve improved guarantees in the multi-agent learning setting. The proof of our upper bound uses a new technique centered around an adaptive choice of potential function at each iteration. We also show that the O(1/√T) rate is tight for all p-SCLI algorithms, which includes OG as a special case. As a byproduct of our lower bound analysis we additionally present a proof of a conjecture of Arjevani et al. (2015) which is more direct than previous approaches.