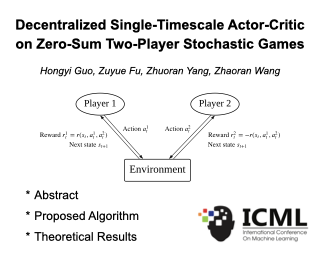
Abstract:
We study discrete-time mean-field Markov games with infinite numbers of agents where each agent aims to minimize its ergodic cost. We consider the setting where the agents have identical linear state transitions and quadratic cost func- tions, while the aggregated effect of the agents is captured by the population mean of their states, namely, the mean-field state. For such a game, based on the Nash certainty equivalence principle, we provide sufficient conditions for the existence and uniqueness of its Nash equilibrium. Moreover, to find the Nash equilibrium, we propose a mean-field actor-critic algorithm with linear function approxima- tion, which does not require knowing the model of dynamics. Specifically, at each iteration of our algorithm, we use the single-agent actor-critic algorithm to approximately obtain the optimal policy of the each agent given the current mean- field state, and then update the mean-field state. In particular, we prove that our algorithm converges to the Nash equilibrium at a linear rate. To the best of our knowledge, this is the first success of applying model-free reinforcement learn- ing with function approximation to discrete-time mean-field Markov games with provable non-asymptotic global convergence guarantees.