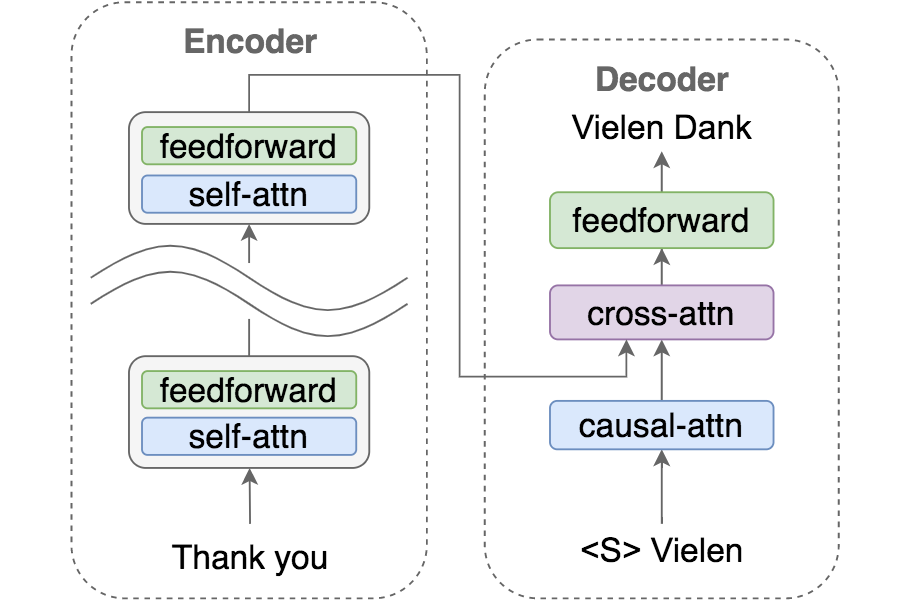
Abstract:
Attention-based architectures have become ubiquitous in machine learning.
Yet, our understanding of the reasons for their effectiveness remains limited.
This work proposes a new way to understand self-attention networks: we show that their output can be decomposed into a sum of smaller terms---or paths---each involving the operation of a sequence of attention heads across layers.
Using this path decomposition, we prove that self-attention possesses a strong inductive bias towards "token uniformity". Specifically, without skip connections or multi-layer perceptrons (MLPs), the output converges doubly exponentially to a rank-1 matrix. On the other hand, skip connections and MLPs stop the output from degeneration. Our experiments verify the convergence results on standard transformer architectures.