Abstract:
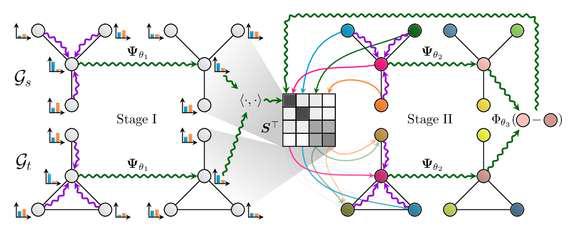
Optimal Transport (OT) for structured data has received much attention in the machine learning community, especially for addressing graph classification or graph transfer learning tasks. In this paper, we present the Diffusion Wasserstein (\(\mathtt {DW}\)) distance, as a generalization of the standard Wasserstein distance to undirected and connected graphs where nodes are described by feature vectors. \(\mathtt {DW}\) is based on the Laplacian exponential kernel and benefits from the heat diffusion to catch both structural and feature information from the graphs. We further derive lower/upper bounds on \(\mathtt {DW}\) and show that it can be directly plugged into the Fused Gromov Wasserstein (\(\mathtt {FGW}\)) distance that has been recently proposed, leading - for free - to a DifFused Gromov Wasserstein distance (\(\mathtt {DFGW}\)) that allows a significant performance boost when solving graph domain adaptation tasks.